皆さん、こんにちは!
以前の記事「指数を使えるようになろう!」では、2^3 のように「同じ数を何回か掛ける」便利な計算方法として指数を学びましたね。
しかし、指数が持つ力は、単なる計算のショートカットだけではありません。実は、物事の「変化のダイナミズム」を捉えるという、もっとスケールの大きな役割を担っているのです。
試しに、2を1回掛ける(2^1)、2回掛ける(2^2)、3回、4回……と考えてみましょう。その値はどのように増えていくでしょうか?
2, 4, 8, 16, 32, \dots
最初は穏やかに見えますが、回数を重ねるごとに、その増加は爆発的になっていきます。この「急激な伸び方」こそが、指数の本質的な特徴です。
今回は、この変化の様子を「グラフ」という形で可視化することで、指数を「関数」として捉え直してみたいと思います。グラフのカーブの先に、指数の新しい世界が広がっています。さあ、一緒に探求していきましょう!
指数についての復習
本題に入る前に、まずは「指数」の基本的なルールを短くおさらいしましょう。
指数とは、ある数のかけ算をコンパクトに表現する方法でしたね。
例えば、3を3回掛け合わせる計算は、次のように書きます。
3 \times 3 \times 3 = 3^3
この右肩に乗っている小さな数字が指数です。
さて、ここからが重要です。
指数関数を扱う準備として、指数が「0、負の数、分数」の場合も考えられるように、その世界を広げておきましょう。
これからの議論では、底(てい)と呼ばれる土台の数字aは正の数(a > 0)とします。
■ ゼロ乗 → 1
どんな数も0乗すると、例外なく 1 になります。
a^0 = 1
■マイナス乗 → 逆数
マイナス乗は「逆数にする」というサインです。
例えば、-2乗なら「2乗したものの逆数」と考えます。
a^{-x} = \frac{1}{a^x}
■分数乗 → ルート(累乗根)
\frac{1}{2}乗は平方根(\sqrt{\phantom{a}})、\frac{1}{3}乗は3乗根(\sqrt[3]{\phantom{a}})を表します。
a^{\frac{1}{x}} = \sqrt[x]{a}
そして、指数計算には指数法則という強力なルールがありました。
例えば、次のようなものです。
a^x \times a^y = a^{x+y}\\
(a^x)^y = a^{xy}
これらの法則のおかげで、複雑な計算もシンプルに扱えるのでした。
より詳しい復習は、前回の記事「指数を使えるようになろう!」にまとめてありますので、不安な方はそちらもご覧ください。
指数を「関数」として見てみよう
ここまでは、「 2^4は16」というように、指数を固定された回数の掛け算として見てきました。
ここで、視点をガラリと変えてみましょう。
右肩に乗せる数(指数)を、固定の数ではなく自由に変えられる数だと考えたらどうなるでしょうか?
例えば、底を「2」に固定して、指数に入れる数をx、計算結果をy としてみます。
すると、この関係は次のような式で表せますね。
y = 2^x
この式で、x に様々な値を入れてみましょう。
- x=1 のとき、y=2^1=2
- x=2 のとき、y=2^2=4
- x=3 のとき、y=2^3=8
- x=0 のとき、y=2^0=1
- x=−1 のとき、y=2^{−1}=0.5
このように、x の値を一つ決めると、それに対応して y の値がただ一つに決まります。
思い出してください。
このように「ある数(入力)を入れると、別の数(出力)が一つ決まる仕組み」、これこそが「関数」の正体でした。
そして、y=2^x のように、変数が指数の部分にある関数のことを、その名の通り「指数関数」と呼びます。
このように指数を関数として見ることで、単なる計算のルールが「変化の様子を捉えるための道具」へと進化するのです。
その最大のメリットは、様々なx の値に対する変化の様子を、グラフを使ってひと目で理解できるようになることです。
さあ、これで準備は整いました。
ここからは、この指数関数がどのような姿形をしているのか、グラフを描いて明らかにしていきましょう!
Pythonでグラフを描いてみよう
前の章で登場した「指数関数」。
それがどんな姿をしているのか、実際にグラフを描いて目で見て確かめていきましょう!
グラフ描画には、Pythonの matplotlib と、数値計算を効率的に行う numpy という2つのライブラリを使います。もしまだインストールしていなければ、以下のコマンドで準備してください。
pip install matplotlib numpy
まずは一番シンプルな指数関数y = 2^xのグラフを描いてみます。
import numpy as np
import matplotlib.pyplot as plt
def plot_exp_func(base):
"""底 base の指数関数 y = base^x をプロットする"""
x = np.linspace(-2, 5, 100) # -2から5までを100分割
y = base ** x # 指数関数を計算
plt.plot(x, y, label=rf"$y={base}^{{x}}$") # xとyの配列からグラフを作成
return x, y # 拡張性のため
def setup_graph(title, xlabel="x", ylabel="y"):
"""グラフの基本的な装飾を設定する関数"""
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.axhline(y=0, color='black', linewidth=1.5) # x軸
plt.axvline(x=0, color='black', linewidth=1.5) # y軸
plt.grid(True)
plt.legend()
plt.show()
if __name__ == '__main__':
# 日本語フォント(環境に応じて変更)
plt.rcParams['font.family'] = 'Meiryo'
# 指数関数のプロット
x, y = plot_exp_func(2) # y = 2^xのグラフ
# グラフの装飾
setup_graph("指数関数のグラフ")
これを実行すると、次のようなグラフが表示されます。
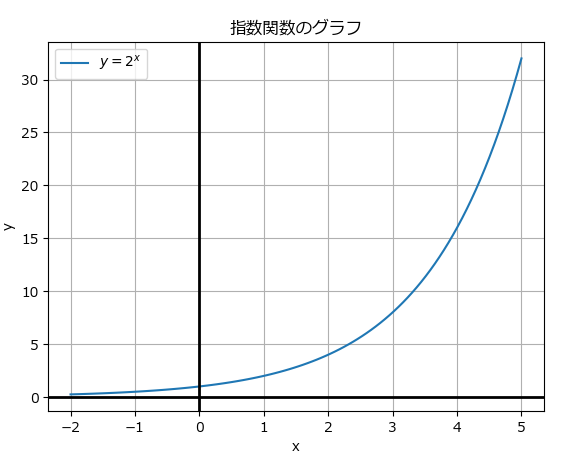
このグラフをじっくり眺めると、いくつかの重要な特徴が読み取れます。
- 必ず点 (0, 1) を通る(x = 0の時、y=1となるため)。
- xが大きくなるほど、yは爆発的に増加していく。
- xが負の方向に進むと、yは 0 に限りなく近づいていく(しかし、決して 0 にはなりません)。
この「xが増えれば yも増える」性質を単調増加、「限りなく近づくけれど交わらない線」を漸近線(この場合はy=0すなわちx軸)と呼びます。
次に、底aの値を変えるとグラフはどう変わるのか、比べてみましょう。
底が1より大きい y=2^x, y=3^x と、1より小さい y=0.5^x を重ねて描いてみます。
import numpy as np
import matplotlib.pyplot as plt
def plot_exp_func(base):
"""底 base の指数関数 y = base^x をプロットする"""
x = np.linspace(-3, 3, 100) # -3から3までを100分割
y = base ** x # 指数関数を計算
plt.plot(x, y, label=rf"$y={base}^{{x}}$") # xとyの配列からグラフを作成
return x, y # 拡張性のため
def setup_graph(title, xlabel="x", ylabel="y"):
"""グラフの基本的な装飾を設定する関数"""
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.axhline(y=0, color='black', linewidth=1.5) # x軸
plt.axvline(x=0, color='black', linewidth=1.5) # y軸
plt.grid(True)
plt.legend()
plt.show()
if __name__ == '__main__':
# 日本語フォント(環境に応じて変更)
plt.rcParams['font.family'] = 'Meiryo'
# 指数関数のプロット
x1_2, y1_2 = plot_exp_func(0.5) # y = 0.5^xのグラフ
x2, y2 = plot_exp_func(2) # y = 2^xのグラフ
x3, y3 = plot_exp_func(3) # y = 3^xのグラフ
# グラフの装飾
setup_graph("指数関数のグラフ")
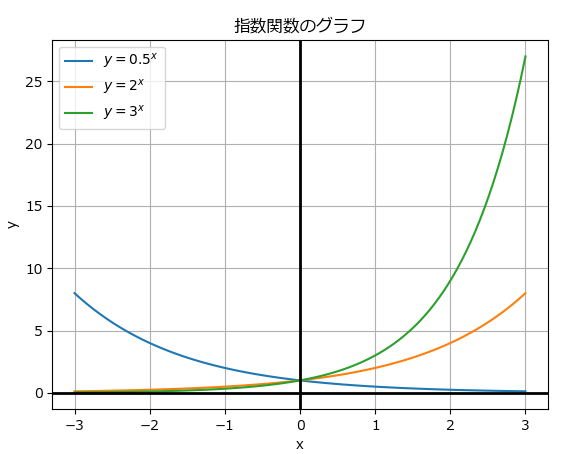
このグラフから、指数関数y = a^x の性質がよりハッキリと分かりますね。
- a > 1 の時 : aの値が大きいほど、グラフの立ち上がりが急になります(y=3^xはy=2^xより急)。
- 0 < a < 1の時 : グラフは右肩下がり、つまり単調減少します。xが増えるとyは0に近づいていきます。
底aの大きさが、関数の「勢い」を決めているのが分かります。
「爆発的に増える」と言われても、いまいちピンと来ないかもしれません。
そこで、私たちに馴染み深い1次関数y=xと比べて、その凄さを体感してみましょう。
import numpy as np
import matplotlib.pyplot as plt
def plot_exp_func(base):
"""底 base の指数関数 y = base^x をプロットする"""
x = np.linspace(-2, 6, 100) # -2から6までを100分割
y = base ** x # 指数関数を計算
plt.plot(x, y, label=rf"$y={base}^{{x}}$") # xとyの配列からグラフを作成
return x, y # 拡張性のため
def plot_linear_func(slope, intercept):
"""1次関数 y = ax + b をプロットする関数"""
x = np.linspace(-2, 6, 100) # -2から6までを100分割
y = slope * x + intercept
plt.plot(x, y, label=rf"$y={slope}x + {intercept}$")
return x, y
def setup_graph(title, xlabel="x", ylabel="y"):
"""グラフの基本的な装飾を設定する関数"""
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.axhline(y=0, color='black', linewidth=1.5) # x軸
plt.axvline(x=0, color='black', linewidth=1.5) # y軸
plt.grid(True)
plt.legend()
plt.show()
if __name__ == '__main__':
# 日本語フォント(環境に応じて変更)
plt.rcParams['font.family'] = 'Meiryo'
# 指数関数のプロット
x2, y2 = plot_exp_func(2) # y = 2^xのグラフ
xl, yl = plot_linear_func(1, 0) # y = xのグラフ
# 軸線を太く描画(x=0, y=0)
plt.axhline(y=0, color='black', linewidth=2)
plt.axvline(x=0, color='black', linewidth=2)
# グラフの装飾
setup_graph("指数関数のグラフ")
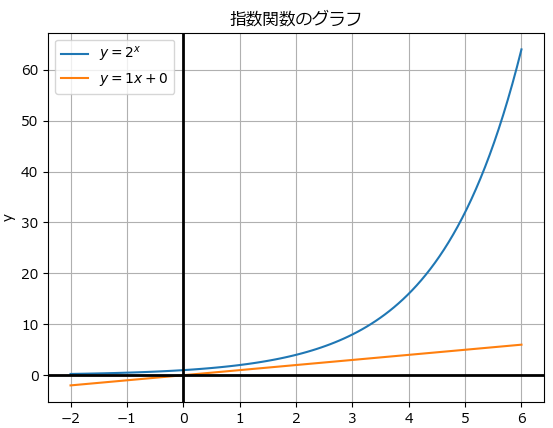
どうでしょうか。
最初は1次関数y=xとy=2^xはほぼ同じくらいの位置にいますが、xが少し増えただけでy=2^xはあっという間にy=xを引き離し、天高く突き抜けていきます。
これが指数関数的な増加の恐ろしさ、そして面白さです。
まとめ
今回は、単なる計算の道具だった「指数」を、グラフという強力な武器を使って「指数関数」として探求してきました。
最後に、今回の冒険で分かったことを振り返ってみましょう。
- y=a^xのように指数を関数として捉えることで、静的な計算が「x の変化に応じて y がどう変わるか」というダイナミックな変化の物語へと変わりました。
- Pythonでグラフを可視化することで、指数関数の重要な性質を直感的に理解できました。
・必ず点 (0, 1) を通る。
・底がa>1なら爆発的に増加し、aが大きいほどその勢いは増す。
・底が0<a<1 なら急速に減少する。
・y=xのような1次関数とは比べ物にならないほどの、凄まじい増加率を持つ。
「指数関数的な成長」という言葉を耳にすることがありますが、その本当の凄みの一端を、グラフの急激なカーブから感じていただけたのではないでしょうか。
さて、グラフの形は分かりましたが、この「爆発的な増加」は一体どれほど強力で、私たちの世界でどのように使われているのでしょうか。
次回は「指数関数って何がスゴいの?」をテーマに、その正体にもっと深く迫っていきたいと思います。
最後までお読みいただき、ありがとうございました!