皆さん、こんにちは!
前回の記事「指数のグラフを描いてみよう ―「数をかける」とどう変化する?」では、Pythonを使って指数関数のグラフを描き、その基本的な形を学びました。
右肩上がりの急なカーブが印象的でしたね。
今回は、「で、結局その指数関数って何がそんなにスゴいの?」という疑問に答えるべく、その爆発的な増加の本質と、私たちの世界との意外なつながりに迫ります。
指数関数の定義と性質の復習
まず、指数関数の定義と性質を復習しましょう。
指数関数は、一般的に以下の形で表されます。
y = a^x
ここで、aは底と呼ばれ、a \neq 1かつa > 0を満たす定数です。
xが変数になります。
指数関数の性質としては以下があります。
- 必ず(0,1)を通る
- x軸(y=0が漸近線になる
- a > 1の時、グラフは単調増加
- 0 < a < 1の時、グラフは単調減少
指数関数ってどこで出てくるの?
実は、指数関数は数学の世界を飛び出して、身の回りの至る所に潜んでいます。
- 複利計算:銀行預金の利息が利息を生む「複利」の増え方は、まさに指数関数です。
- 生物の増殖:ウイルスや細菌が分裂して増えていくスピードも、理想的な環境では指数関数的に増加します。
- 情報拡散:SNSで面白い投稿が「バズる」時の拡散の仕方も、指数関数的なモデルで説明されることがあります。
このように、「ある量が増えるほど、さらに増えるスピードも速くなる」という性質を持つ現象は、指数関数と深く結びついているのです。
リニア vs エクスポネンシャル
指数(エクスポネンシャル)関数の「爆発力」を体感するために、最もシンプルな「線形(リニア)な増加」と比較してみましょう。
ここに2人の若者がいます。
B君(エクスポネンシャル):初日は1円だけもらい、次の日からはその倍額を毎日もらい続ける。
A君(リニア):毎日1万円ずつ、コツコツ貯金する。
どちらが多く貯金できると思いますか?
最初の数日をみてみましょう。
| 日数 | A君の合計貯金額 | B君の合計貯金額 |
| 1日目 | 10,000円 | 1円 |
| 2日目 | 20,000円 | 3円 |
| 5日目 | 50,000円 | 31円 |
| 10日目 | 100,000円 | 1,023円 |
10日目の時点ではA君が圧倒的に優勢です。
B君の選択は失敗だったと思いますか?
答えは「No!」です。
ここからが本番です。
30日後、B君とA君の貯金額の差は驚くべき差になっています。
- A君 : 1万円 \times 30日 = 30万円
- B君 : 初項1、公比2の等比数列の和なので、2^30 – 1 = 1,073,741,823円 ≒ 10.7億円
最初はA君の方が圧倒的に優勢でしたが、その差はみるみる縮まり、18日目でB君の貯金額がA君を超えます。
その後は比較にならないほど差が巨大になっていきます。
これが指数関数的な増加の本質です。
チェス盤と米粒の話
この指数関数の爆発力を示す、有名な昔話があります。
「チェス盤と米粒の話」というものです。
チェスを発明した賢者(多くの場合はインドでとされる)は、その褒美として王様から褒美を与えられることになりました。
賢者はこう言いました。
「陛下のチェス盤の最初のマスに米粒を1粒、次のマスには2粒、その次のマスには4粒…と、マス目が進むごとに倍の数の米粒をください。64マス分、それで十分でございます。」
王様は
「なんと謙虚なことだ」
と、その願いを快く受け入れました。
さて、王様が賢者に支払う米粒の合計は何粒になったのでしょうか?
Pythonを使って計算してみましょう。
その際にマス目を横軸に、そのマス目に置かれる米粒の数を縦軸にしてグラフを作ってみましょう。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
# y軸の目盛りを「数値 × 10^n」形式に変換する関数
def custom_scientific_formatter(y, pos):
"""y軸の目盛りをカスタムの科学技術表記にフォーマットします。"""
if y == 0:
return "0"
# 10を底とする指数を計算
exponent = int(np.floor(np.log10(abs(y))))
# 仮数(1から10の間の数)を計算
mantissa = y / (10 ** exponent)
# LaTeXを使って美しい数式として出力
return rf'${mantissa:.1f} \times 10^{{{exponent}}}$'
if __name__ == '__main__':
# 日本語フォントの設定
plt.rcParams['font.family'] = 'Meiryo'
# 数式部分をより美しく表示するためのフォント設定
plt.rcParams['mathtext.fontset'] = 'cm'
# チェス盤のマス目 (1から64)
squares = np.arange(1, 65, dtype=object)
# 各マス目の米粒の数 (2^(n-1))
grains = 2 ** (squares - 1)
# マス目に置かれる米粒の数をprint
for square, grain in enumerate(grains):
print(f"{square+1}番目のマスには{grain}個の米粒")
print(f"米粒の合計 : {sum(grains)}粒")
# グラフの描画
plt.figure(figsize=(10, 7))
plt.plot(squares, grains, marker='o', linestyle='-')
plt.title("チェス盤と米粒:指数関数的な増加")
plt.xlabel("マス目 (n)")
plt.ylabel("そのマスに置かれる米粒の数")
plt.grid(True)
# 作成したカスタムフォーマッターをy軸に適用
ax = plt.gca()
ax.yaxis.set_major_formatter(FuncFormatter(custom_scientific_formatter))
plt.show()
y軸の値を見やすいように10^nという表示ができるようにしています。
やっていることは単純です。
米粒の数は1マス目が1、2マス目が2、それから倍々になるので、初項1、公比2の等比数列になります。
なので、米粒の数 = 2^{\textrm{マス目-1}}となります。
これをプログラムしている部分が
# チェス盤のマス目 (1から64)
squares = np.arange(1, 65, dtype=object)
# 各マス目の米粒の数 (2^(n-1))
grains = 2 ** (squares - 1)
になります。
後はmatplotlib.pyplotを使ってグラフにしています。
このプログラムを実行すると次のような結果になります。
1番目のマスには1個の米粒 2番目のマスには2個の米粒 3番目のマスには4個の米粒 4番目のマスには8個の米粒 ・・・(途中多いので省略) 61番目のマスには1152921504606846976個の米粒 62番目のマスには2305843009213693952個の米粒 63番目のマスには4611686018427387904個の米粒 64番目のマスには9223372036854775808個の米粒 米粒の合計 : 18446744073709551615粒
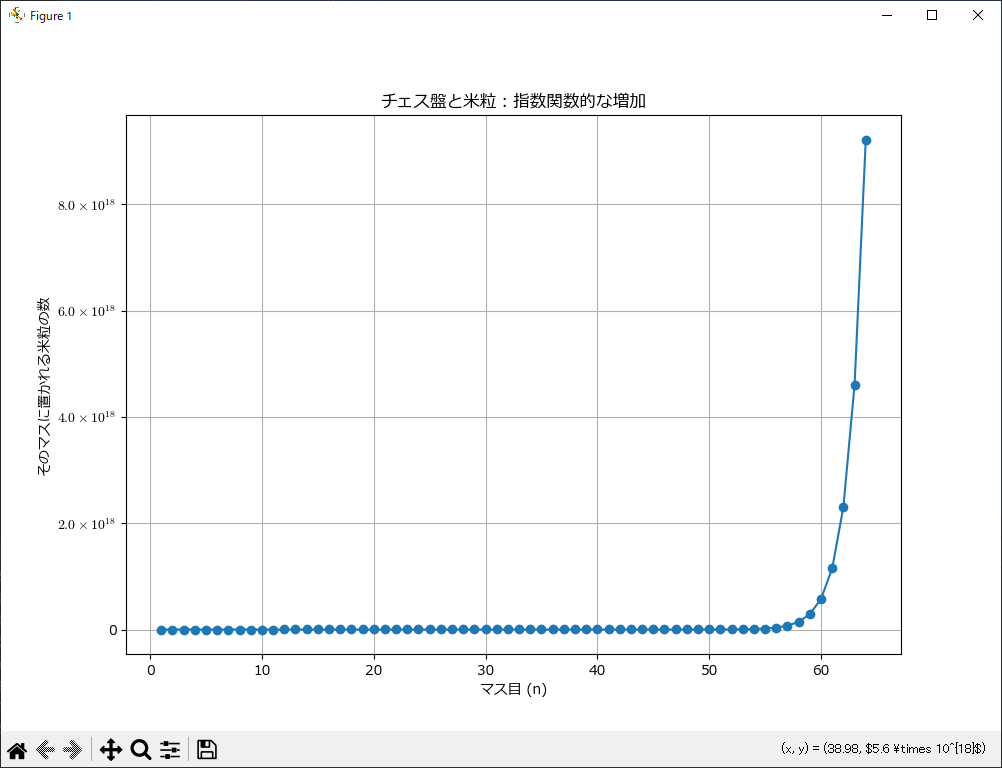
最後の64マスには2^{63}= 9223372036854775808 粒、約922京粒の米が必要になります。
合計では約1844京粒の米が必要になります。
※日本の単位は万→億→兆→京です。
現代の世界全体の米の年間生産量は約8億トンです。
つまり、王様は賢者に世界全体の米の生産量の230億5000万年分にも相当する量を与える約束をしたことになります。
王様は賢者に「なんと謙虚なことだ」と言っていますが、全然謙虚でもなかったんです。
人間の直感が、指数関数の成長率をいかに見誤るかを示す、痛快なエピソードです。
まとめ
今回の記事では、指数関数が持つ「スゴさ」、すなわち爆発的な増加の本質に、様々な角度から迫りました。
■直感とのギャップを体感する
「リニア(線形)な増加」との比較や、「チェス盤と米粒のパズル」という古典的な物語を通して、指数関数的な増加がいかに私たちの直感とかけ離れた、凄まじい結果を生むかを体感しました。
最初はごく僅かな差が、ある時点から決して追いつけないほどの圧倒的な差になるのが特徴です。
■「量が増えるほど、伸びも速くなる」モデル
指数関数のスゴさの核心は、「現在の量に比例して、次の増加量が決まる」という性質にあります。
これは、お金がさらにお金を生む「複利」や、生物が分裂して数を増やす「増殖」など、私たちの世界の様々な現象を説明する強力な数学的モデルとなっています。
■Pythonによる可視化
チェス盤の米粒の増加をPythonでプロットすることで、抽象的な数式が、目で見てわかる急激な曲線へと変わる様子を確認しました。
プログラミングは、こうした数学的な概念を深く理解するための強力なツールとなります。
指数関数を理解することは、単に数学の問題が解けるようになるだけでなく、世の中の様々な変化の裏に隠されたダイナミズムを読み解く「解像度」を上げてくれるのです。