「ちょっと一息、コーヒーでもいかがですか?」
手には温かいマグカップ、お供には甘いドーナツ。
多くの人が経験する、ほっとする瞬間ですね!
でも、もし「そのマグカップとドーナツは数学的には同じ形ですよ」と言われたら、どう思いますか?
「えっ、どう見ても違うでしょ!?」となりますよね?
位相幾何学(トポロジー)という数学の一分野では、この2つは同じ形・同じ仲間だと考えます。
トポロジーは、図形をぐにゃぐにゃと連続的に変形させて同じ形になるものを「同じ」とみなす、「やわらかい幾何学」です。
この記事では、そんな不思議で奥深いトポロジーの世界へとご案内します。
「形の本質」とは何か?一緒に探求していきましょう!
位相幾何学(トポロジー)ってどんな数学?
私たちが普段慣れ親しんでいる幾何学は、図形の「長さ」や「角度」が重要です。
中学校の時に、合同や相似というものを学習したと思います。
合同は、例えば、三角形や四角形が全く同じ形・大きさをしているというものでした。
しかし、図形の形というものの本質に大きさは関係ないのではないかという視点で見た場合の関係が相似でした。
相似な図形は角度は全て同じで、対応する辺の比が全て等しいというものでした。
言い換えると拡大または縮小すると重なり合う形は「同じ」とみなしたものでした。
相似を考えると、確かに「大きさ」は形の本質ではないという気がしてきます。
この考えをもっと進めたものがトポロジーになります。
トポロジーのルールは
「図形を粘土のように、自由に伸ばしたり縮めたりして変形してよい。ただし、ちぎったり、新しく穴をあけたり、くっつけたりしてはいけない」
というものです。この「連続的な変形」で同じ形にできるものを、トポロジーでは「同相(どうそう)」といい、つまりは同じ形と考えます。
(1) 四角形を連続的に変形すると円になります。
つまり、トポロジーでは四角形と円は同じ形と考えます。
下は四角形から丸へ連続変形していくアニメーションです。

(2) 立方体を中から膨らますように変形すると球になります。
つまり、トポロジーでは立方体と球は同じ形と考えます。

トポロジーでは、「辺の数」や「角度」が大切なのではなく、「つながり方」が重要になります。
ドーナツからマグカップへ!
では、本題のドーナツからマグカップへの連続変形を見てみましょう。
どのように変形すればドーナツからマグカップに変形できるでしょうか?
次のアニメーションでマグカップからドーナツへの連続変形を見てください!

どうでしょうか?
一度も切ったり貼ったりすることなく、マグカップからドーナツに変形することができました。この変形の中で、たった1つ変わらなかったものがあります。
それは何だと思いますか?
連続変形で変わらないもの
上の問いに答えましょう。
マグカップからドーナツに変形する際に変わっていないものは、「穴の数」です。
マグカップには取手の部分に穴がありますね。
ドーナツにも真ん中に穴があります。
マグカップからドーナツへの連続変形でこの穴の数は1つのまま変わっていません。
この穴の数のことをトポロジーでは種数といいます。
種数はドーナツやマグカップのような2次元の図形を分類するための道具になってきます。
例えば、
種数が0の2次元の図形はサッカーボールなどの表面、
種数が1の2次元の図形はドーナツやマグカップの表面などがあります。
トポロジーでは連続変形で変わらないものを「位相不変量」といいます。
トポロジーという分野の最大の目的は、同相である図形を同じ図形とみなし、図形や空間の分類・理解を行うことです。
位相不変量は図形や空間の分類をするための重要な「ものさし」になります。
オイラー標数
種数に関連する面白い位相不変量としてオイラー標数があります。
これは、多面体の頂点(V: Vertex)、辺(E: Edge)、面(F: Face)の数を使ってV – E + Fで計算できます。
頂点の数 : 8個
辺の数 : 12個
面の数 : 6枚
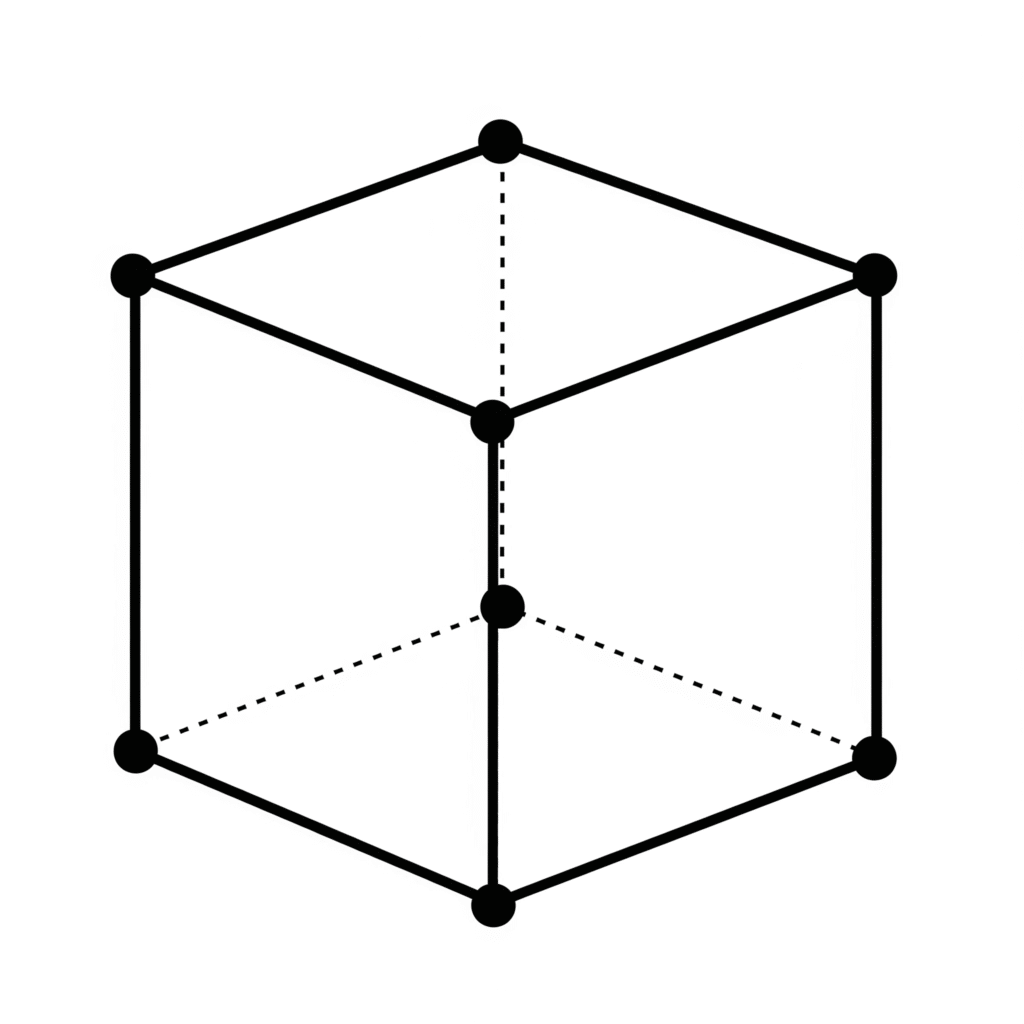
オイラー標数を計算すると 8 – 12 + 6 = 2となります。
実は、球面と同相な図形は、どんな形であってもオイラー標数は必ず2になります。
これをPythonで計算してみましょう。
def calc_euler_characteristic(v, e, f):
"""オイラー標数(頂点の数v - 辺の数e + 面の数f)を計算"""
return v - e + f
if __name__ == '__main__':
# 立方体
v_cube = 8
e_cube = 12
f_cube = 6
print(f"立方体のオイラー標数: {calc_euler_characteristic(v_cube, e_cube, f_cube)}")
# 正四面体
v_tetra = 4
e_tetra = 6
f_tetra = 4
print(f"正四面体のオイラー標数: {calc_euler_characteristic(v_tetra, e_tetra, f_tetra)}")
ちなみに、ドーナツの表面に同じように頂点・辺・面を作ってV-E+Fを計算すると、どのように分割しても必ず 0 になります。
この「2」と「0」という値の違いが、球とドーナツが決して同じ形になれないことの数学的な証明になっているのです。
ちなみに、この章のはじめにオイラー標数が種数と関連があると言っていますが、実は種数gとオイラー標数Xの間にはX = 2 – 2gという関係が成り立ちます。
トポロジーの以外な応用分野
ドーナツとマグカップの話は、まるで面白い数学パズルのようですよね。
しかし、この「形の本質」を見抜くトポロジーの力は、ただの遊びや思考実験に留まりません。
実は、最先端の科学技術を支える強力な武器として、様々な分野で応用されているのです。
- ロボット工学:賢い経路を見つける力
例えば、お掃除ロボットや工場のロボットアームが、障害物を賢く避けながら目的地に到達する経路を考えるとき。
無数にある経路の中で、本質的に「同じ」経路と「違う」経路をどうやって見分ければよいでしょうか?
ここにトポロジーの考え方が活きてきます。
空間の「つながり方」や「障害物の穴」をトポロジー的に捉えることで、ロボットは無駄なく効率的で、かつ安全な動きを計算することができるのです。 - データ解析:データの「形」から隠れたパターンを発見する
トポロジカル・データ解析(TDA)というものがあります。
一見、ただの点の集まりにしか見えない健康診断データや顧客の購買履歴といった複雑なデータも、TDAを使えばその「形」を調べることができます。
データの中に隠されたループ状のパターン(例えば、顧客の周期的な行動)やデータの”隙間”を見つけ出し、従来の統計手法では得られなかった新しい知見を発見するのに役立ちます。 - 物理学:ミクロな世界の法則を記述する言語
物質の性質や宇宙の成り立ちを探る物理学の世界でも、トポロジーは不可欠です。
物質の特殊な電気的性質を説明し、近年のノーベル物理学賞のテーマにもなった「トポロジカル絶縁体」や、この宇宙の最小単位を”ひも”と考える超弦理論など、目には見えないミクロな世界の構造を記述するための言語として、トポロジーは活躍しています。
このように、トポロジーは単なる抽象的な学問ではありません。
それは、ロボットの動きから膨大なデータの海、そして宇宙の法則に至るまで、現実世界の様々な「形」を深く理解するための、強力な知的ツールなのです。
まとめ
トポロジーは、一見複雑に見える世界の「形」の中から、本質的な構造を見つけ出すための強力なレンズです。
- ドーナツとマグカップは「穴が1つ」という本質を共有している。
- トポロジーは「つながり方」に着目する、やわらかい幾何学。
- その考え方は、データサイエンスや物理学など、最先端の分野でも応用されている。
私たちの身の回りには、まだまだ面白い「同じ形」の組み合わせが隠されているかもしれません。