素数にも“リズム”がある？──間隔に注目した素数のビート

「素数っていくつあるの？」では、素数が無限に存在することを紹介しました。
では、そんな素数は、どんな“間隔”で現れるのでしょうか？
完全にバラバラ？それとも、そこに隠れた“リズム”がある？

今回は、素数の間隔に注目して、その不思議な出現パターンを探ってみたいと思います。

Contents

素数は本当にランダムに出現する？
素数の出現間隔（差分）を調べてみよう
なぜ2,4,6が多い？素数の合同類から見える”ビート”
- 素数の差が2,4,6に多い理由
音にしてみたらどうなる？“素数ビート”の試み
まとめ

素数は本当にランダムに出現する？

まずは、Pythonを使って 100未満の素数 を眺めてみましょう。
今回は、数式処理が得意なライブラリ SymPy（シンパイ） を使います。
以下のコマンドでインストールできます。

pip install sympy

SymPy では、primerange という関数を使うことで、指定した範囲の素数を簡単に取得できます。
以下は、2以上100未満の素数をすべて列挙するコードです。

from sympy import  primerange

if __name__ == '__main__':
    primes = list(primerange(2,100)) #100未満の素数をリストで取得
    print(primes)

実行結果は以下のようになります：

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

ここで使用した primerange(a, b) は、a以上b未満の範囲にある素数をイテレータとして返す関数です。
使いやすくするために、list() を使ってリスト化しています。

さて、ここでちょっと面白い視点を加えてみましょう。
素数と素数の間の「差」に注目してみます。

たとえば、最初のいくつかの素数について差を計算すると次のようになります：

3 - 2 = 1  
5 - 3 = 2  
7 - 5 = 2  
11 - 7 = 4  
13 - 11 = 2  
17 - 13 = 4  
19 - 17 = 2  
...（以下略）

差のリストを並べると、以下のようになります：

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8

ぱっと見て、2や4、6といった値がよく登場していることに気づきます。
これは偶然でしょうか？それとも何か法則的な“リズム”があるのでしょうか？

次の章では、この“リズム”の正体を探っていきます。

素数の出現間隔（差分）を調べてみよう

1000未満の素数について、それぞれの間隔（差分）をリストアップし、ヒストグラムにして可視化してみましょう。
ここではグラフの描画に matplotlib を使用しますので、以下のコマンドでインストールしておきましょう。

pip install matplotlib

以下がそのソースコードです。

import matplotlib.pyplot as plt
from sympy import primerange

if __name__ == '__main__':
    # フォント設定（日本語対応）
    plt.rcParams['font.family'] = 'Meiryo'

    # 素数と差の計算
    primes = list(primerange(2, 1000))
    diffs = []  # 空のリストを用意

    for i in range(len(primes) - 1):
        diff = primes[i + 1] - primes[i]  # 2つの素数の差を計算
        diffs.append(diff)  # リストに追加

    # ヒストグラムの表示
    plt.hist(diffs, bins=range(1, max(diffs) + 2), align='left', rwidth=0.8)

    # 横軸を1単位に設定
    plt.xticks(list(range(1, max(diffs) + 1)))

    # ラベルやタイトルを設定
    plt.xlabel('素数間の差')
    plt.ylabel('出現回数')
    plt.title('素数間隔のヒストグラム')

    plt.show()

このプログラムは、以下のような流れで処理を行っています。

primerange 関数を使って、1000未満の素数をリスト化
連続する素数同士の差を計算し、diffs というリストに格納
matplotlib.pyplot を使って、その差をヒストグラムとして可視化

このプログラムを実行すると、以下のようなヒストグラムが表示されます

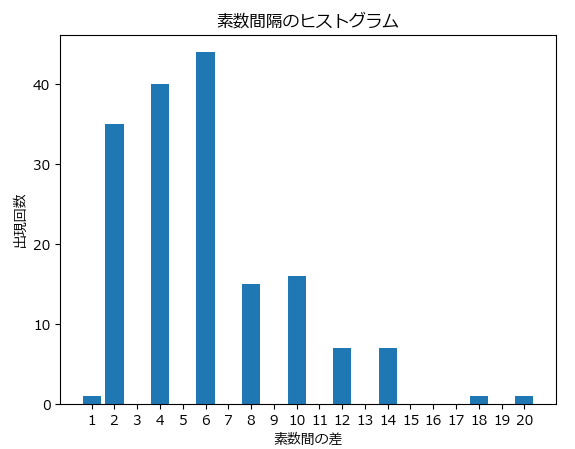
グラフを見ると、差が 2・4・6 の素数ペアが特に多く出現していることがわかります。

これは偶然なのでしょうか？
実は、この背景には素数に特有の“ある性質”が隠れているのです。

それを次の章で探っていきましょう！

なぜ2,4,6が多い？素数の合同類から見える”ビート”

素数は2と3と除くと、「 $6n \pm 1$ 」という形をしています。

すべての自然数は次のいずれかの形に分類できます（6で割った余りを考えます）。
以下, $n$ は自然数とします。

$6n$
$6n+1$
$6n+2$
$6n+3$
$6n+4$
$6n+5$

この中で、どの形が素数になり得るかを見ていきましょう。

$6n$ の場合
6の倍数なので、明らかに素数ではありません。
（ $n=1$ なら 6、 $n=2$ なら 12 など）

$6n+1$ の場合
素数になる可能性があります。
例 : 7,13,19など。

$6n+2$ の場合
$2(3n+1)$ となり、2の倍数です。
従って、 $n=0$ のときの2を除き、素数にはなりません。

$6n+3$ の場合
$3(2n+1)$ となり、3の倍数です。
同様に、 $n=0$ のときの3を除き、素数にはなりません。

$6n+4$ の場合
$2(3n+2)$ となり、偶数になります。
素数にはなりません。

$6n+5$ の場合
$6(n+1)-1$ と変形でき、 $6k-1$ の形になります。
素数になる可能性があります。
例 : 5,11,17,23など。

以上より、2と3の場合を除くと、素数になり得るのは $6n+1$ と $6n+5 = 6k-1$ の形だけに限られることがわかります。

ただし注意すべきは、この逆は成り立たないという点です。
つまり、「 $6n \pm 1$ 」の形だからといって、必ず素数であるわけではない」ということです。
例 :

$6n+1 = 24+1 = 25 = 5^2$ ( $n=4$ のとき)
$6n-1 = 36-1 = 35 = 5 \times 7$ ( $n=6$ のとき)

よって、「 $6n \pm 1$ 」の形は素数であるための必要条件ではありますが、十分条件ではないのです。

素数の差が2,4,6に多い理由

3 より大きい素数は $6n \pm 1$ の形をしているため、素数同士の差も一定のパターンを持ちます。

以下のように、 $6n+1$ や $6n-1$ 同士の差を場合分けしてみましょう。

$(6n+1) - (6m+1)$ の場合
差は $6(n-m)$ となり、6の倍数になります。
例 : 13 – 7 = 6、19 – 13 = 6

$(6n-1) - (6m-1)$ の場合
差は $6(n-m)$ となり、6の倍数になります。
例 : 17 – 5 = 12、29 – 17 = 12

$(6n+1) - (6m-1)$ の場合
差は $6(n-m)+2$ となり、6で割ると2余る数になります。
例 : 7 – 5 = 2、13 – 11 = 2

$(6n-1) - (6m+1)$ の場合
差は $6(n-m-1)+4$ となり、6で割ると4余る数になります。
例 : 11 – 7 = 4、41 – 37 = 4

このように、3 より大きい素数の差は常に：

6の倍数（0 mod 6）
6で割って2余る数（2 mod 6）
6で割って4余る数（4 mod 6）

のいずれかになります。

つまり、素数の差として現れる数には強い制約があるのです。
差が 1 や 3、5 といった「奇数」で現れることはありません。

この制約のもとで、もっとも小さい差である 2・4・6 は、隣接する素数の差として頻繁に登場するのも自然な結果といえるでしょう。

音にしてみたらどうなる？“素数ビート”の試み

「素数には”リズム”がある」と聞いて、あなたは信じられますか？
これまで私たちは、素数の“間隔”を視覚的にヒストグラムで観察してきました。
今度はそれを音に変換して、耳で感じてみることにしましょう。
──そう、“素数の音楽”を作ってみるのです。

プログラムの解説
音に変換する対象は、前の章でも使用した、隣接する素数同士の差を並べたリスト diffs です。
この差分に基づいて周波数を決定します。
ここでは簡単なルールとして、差が小さい場合は高い音、差が大きい場合は低い音になるように設定しています。
（つまり、リズムが細かくなるほど音が鋭くなるようなイメージです。）
以下は、Windows限定（winsound モジュール使用）のPythonプログラムです：

import time
import winsound
from sympy import primerange

if __name__ == '__main__':
    # 素数間隔を取得
    primes = list(primerange(2, 1000))
    diffs = [primes[i + 1] - primes[i] for i in range(len(primes) - 1)]

    # 差分を音の周波数に変換（例：2→900Hz、6→700Hzなど）
    for diff in diffs:
        freq = 1000 - diff * 50  # 差が大きいと低い音になる
        duration = 100  # ミリ秒
        winsound.Beep(max(200, freq), duration) #音を鳴らす
        time.sleep(0.1)  # 次の音まで少し間をあける

素数が奏でる音楽は、どんな響きがしましたか？