皆さんは有名なコラッツ予想をご存知でしょうか?
予想の内容は中学生でも理解できるような内容ですが、まだ未解決の問題です。
今回は、そのコラッツ予想を体験してみたいと思います。
コラッツ予想
コラッツ予想
まず、コラッツ予想を紹介します。
aを正の整数とする。
a_1 = aとして、次のようにa_nを定義する。
a_{n+1} =
\begin{dcases}
a_n/2 & (a_n \equiv 0 \pmod{2}) \\
3a_n+1 & (a_n \equiv 1 \pmod{2})
\end{dcases}
この時、任意のaに対して、a_m=1となるmが存在する。
コラッツ予想はどんな整数aからスタートしても、
- 奇数なら3倍して1を足す
- 偶数なら2で割る
という操作を繰り返しているうちに、必ず1になるという予想です。
コラッツ予想の具体例
いくつか具体例で見てみましょう!
以下、簡単のために
操作(i)を3倍して1を足す
操作(ii)を2で割る
とします。
a = 3の時
3 \overset{\mathrm{(i)}}{\to} 10 \overset{\mathrm{(ii)}}{\to} 5 \overset{\mathrm{(i)}}{\to}16 \overset{\mathrm{(ii)}}{\to} 8 \overset{\mathrm{(ii)}}{\to} 4 \overset{\mathrm{(ii)}}{\to} 2 \overset{\mathrm{(ii)}}{\to} 1
例1
a = 11 の時
11 \overset{\mathrm{(i)}}{\to} 34 \overset{\mathrm{(ii)}}{\to} 17 \overset{\mathrm{(i)}}{\to} 52 \overset{\mathrm{(ii)}}{\to} 26 \overset{\mathrm{(ii)}}{\to} 13 \overset{\mathrm{(i)}}{\to} 40 \overset{\mathrm{(ii)}}{\to} 20 \overset{\mathrm{(ii)}}{\to} 10 \overset{\mathrm{(ii)}}{\to} 5 \overset{\mathrm{(i)}}{\to} 16 \overset{\mathrm{(ii)}}{\to} 8 \overset{\mathrm{(ii)}}{\to} 4 \overset{\mathrm{(ii)}}{\to} 2 \overset{\mathrm{(ii)}}{\to} 1
ステップ数は多いですが、計算自体は簡単なので実際にいくつかの数値で計算してみて1になることを確かめてみてください!
Pythonで可視化してみよう
実際に計算してみるとステップ数が多いので少し面倒ではあります。
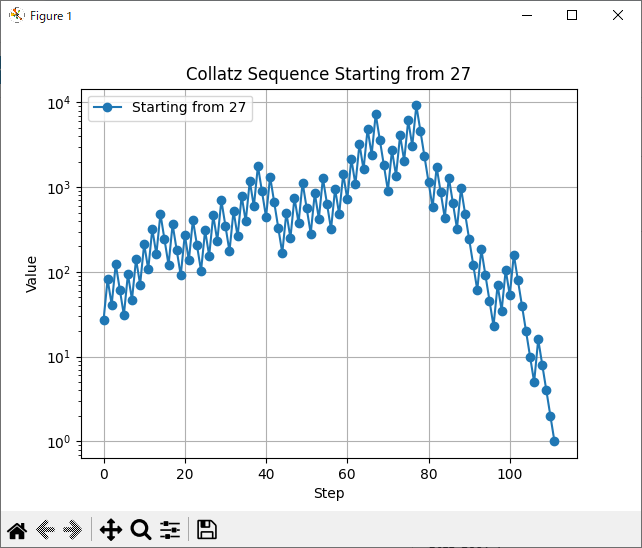
特に、有名な初期値が「27」は1に到達するまでのステップ数が「111回」で、途中に「9232」という非常に大きな値まで増加します。
ここではPythonを使って、この「27」が1に到達するまでを計算して、可視化してみたいと思います。
可視化するためにmatplotlibを使用しています。
pip install matplotlibとし、インストールをしてください。
import matplotlib.pyplot as plt
def collatz_sequence(n):
"""
与えられたnから始まるコラッツ数列を生成する。
:param n: 正の整数
:return: コラッツ数列のリスト
"""
sequence = [n]
while n != 1:
if n % 2 == 0:
n //= 2
else:
n = 3 * n + 1
sequence.append(n)
return sequence
def print_collatz_sequence(sequence):
"""
与えられたコラッツ数列をコンソールに出力する。
:param sequence: コラッツ数列
"""
for i, value in enumerate(sequence):
print(f"Step {i}: {value}")
def show_collatz_sequence(n):
"""
nから始まるコラッツ数列を生成し、プロットする。
:param n: 正の整数
"""
sequence = collatz_sequence(n)
print_collatz_sequence(sequence)
plt.plot(sequence, marker='o',label=f'Starting from {n}')
plt.title(f'Collatz Sequence Starting from {n}')
plt.xlabel('Step')
plt.ylabel('Value')
plt.yscale('log') # Use logarithmic scale for better visibility
plt.grid(True)
plt.legend()
plt.show()
if __name__ == "__main__":
show_collatz_sequence(27)
この結果が
Step 0: 27 Step 1: 82 Step 2: 41 Step 3: 124 Step 4: 62 Step 5: 31 ・・・(長いので省略) Step 74: 2051 Step 75: 6154 Step 76: 3077 Step 77: 9232 (最大値) Step 78: 4616 Step 79: 2308 ・・・(長いので省略) Step 109: 4 Step 110: 2 Step 111: 1
となり、ステップ数とその時のa_nをグラフ化したものが次になります。
ソースコードの内容としては、collatz_sequence関数が全てです。
与えられた初期値nに対して、1になるまでコラッツ予想の時に述べた操作を行っていきます。
その1つ1つの計算の際に算出された値を配列に追加していっています。
コラッツ予想についての補足
コラッツ予想はまだ未解決の問題です。
ただ、コンピューターで計算した結果2^{68}程度までの初期値では、最終的に1に到達することが確認されています。
ただ、できる数字を増やしていってもコラッツ予想が正しいと証明することはできません。
なぜなら整数は無限大にあるからです。
コラッツ予想には「1億2000万円」という懸賞金がかけられています。
有名な「ミレニアム問題」が1問解くと100万ドルでしたので、これに近い賞金ですね!
まとめ
今回は、数学の未解決問題 「コラッツ予想」 を紹介しました。
与えられた初期値から始めて、奇数なら 3n+1、偶数なら n/2を1になるまで繰り返すだけ。
この手続きがすべての正の整数で必ず1に到達するのか――それが「コラッツ予想」です。
実際に具体的な初期値で計算すると多くが1に落ちますが、
「計算で確かめられること」 と 「一般に成り立つこと(証明)」 は別物。
局所的な規則は単純でも、全体の振る舞いを一般化して示すのが難しく、いまも未解決のままです。
最後まで読んでいただき、ありがとうございました。