こんにちは！
皆さん、円周率 $\pi$ は知っていますよね？

円の直径に対する円周の長さの比率のことですね！
無理数で、小中学校の時に3.141592…と覚えたりしてましたよね。

学校では「円周 = 直径 $\times ~ \pi$ 」などの公式を学習しますが、この $\pi$ 自体の値って、どうやって正確に求めたのでしょう？

「円に内接する多角形を使う方法」や「級数展開を使う方法」などにより、過去の偉人たちは円周率を計算をしてきました。

今回は、難しい話は一切なしで、もっと直感的で、「神頼み」なランダムな方法で $\pi$ を求めてみます。
その方法は「モンテカルロ法」！
カジノで有名な地名が由来なんて、ちょっとわくわくしますよね！

Contents

モンテカルロ法
- アイデアは「ダーツ投げ」
- 数式で見てみる
プログラムで $\pi$ を求めて見よう
まとめ

モンテカルロ法

モンテカルロ法は、乱数を用いて試行を繰り返し、数値計算や問題の近似解を求める手法です。
関数や数式の解析的な解が難しい場合に、ランダムに多数の入力を与え、その出力を統計的に処理して推定結果を得ることができます。

と、難しい話はここまでにして、

アイデアは「ダーツ投げ」

円周率 $\pi$ をモンテカルロ法で求める方法は、

1辺の長さが2の正方形を用意 (中心が(0,0)で、xもyも-1から1の範囲)
その正方形の中に、半径1の円をぴったりと書く
この正方形の中に、ランダムに点を打っていく

イメージは、四角の中に目隠ししながらダーツを投げるかんじです。

さて、たくさんダーツを投げた時、「円の中に入ったダーツの数」と「正方形の中に入ったダーツの数 (つまり全数)」の比率は、どうなると思いますか？

直感的に分かるかもしれませんが、この比率は「円の面積」と「正方形の面積」の比率に近づきます。

数式で見てみる

つまり、

正方形の面積 : $2 \times 2 = 4$
円の面積 : $\pi \times 1^2 = \pi$

なので、

\frac{\textrm{円の面積}}{\textrm{正方形の面積}} = \frac{\pi}{4}

となり、

\frac{\textrm{円の中に入った点の数}}{\textrm{全ての点の数}} \approx \frac{\pi}{4}

となるはずです。

この両辺を4倍すると

\pi \approx 4 \times \frac{\textrm{円の中に入った点の数}}{\textrm{全ての点の数}}

なので、 $\pi$ の近似値を求める式が完成します。

プログラムで $\pi$ を求めて見よう

Pythonで求めてみよう

それでは、モンテカルロ法で $\pi$ を近似したいと思います。
また、視覚的にも分かるようにmatplotlibで点を打ってみます！

import random
import matplotlib.pyplot as plt


def generate_points(num_points) -> tuple[list[tuple[float, float]], list[tuple[float, float]]]:
    """
    指定された数の点を生成し、円内と円外に分ける関数
    :param num_points: 生成する点の数
    :return: 円内の点のリストと円外の点のリスト
    """
    points_inside = []
    points_outside = []
    for _ in range(num_points):
        # -1から1の範囲でランダムな点を生成
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)
        # 原点からの距離の2乗を計算
        distance_squared = x**2 + y**2
        # 距離の2乗が1以下なら円の中
        if distance_squared <= 1:
            points_inside.append((x, y))
        else:
            points_outside.append((x, y))
    return points_inside, points_outside

def calculate_pi(points_inside, num_points) -> float:
    """
    円内の点の数から円周率を計算する関数

    :param points_inside: 円内の点のリスト
    :param num_points: 生成した点の総数
    :return: 推定された円周率
    """
    inside_circle = len(points_inside)
    pi_estimate = 4 * inside_circle / num_points
    return pi_estimate

def plot_points(points_inside, points_outside, num_points, pi_estimate):
    """
    点をプロットする関数

    :param points_inside: 円内の点のリスト
    :param points_outside: 円外の点のリスト
    :param num_points: 生成した点の総数
    :param pi_estimate: 推定された円周率
    """
    points_inside_x, points_inside_y = zip(*points_inside) if points_inside else ([], [])
    points_outside_x, points_outside_y = zip(*points_outside) if points_outside else ([], [])
    plt.figure(figsize=(6, 6))
    plt.scatter(points_inside_x, points_inside_y, color='blue', s=1, label='Inside Circle')
    plt.scatter(points_outside_x, points_outside_y, color='red', s=1, label='Outside Circle')
    
    # 正方形を描く
    plt.plot([-1, 1, 1, -1, -1], [-1, -1, 1, 1, -1], 'k-', linewidth=2, label='Square')
    
    # 円を描く
    circle = plt.Circle((0, 0), 1, fill=False, color='black', linewidth=2, label='Circle')
    plt.gca().add_artist(circle)
    
    plt.title(f'N = {num_points}, Estimated Pi = {pi_estimate:.6f}')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.axis('equal')
    plt.xlim(-1.1, 1.1)
    plt.ylim(-1.1, 1.1)
    plt.show()

def main():
    """
    メイン関数
    """
    num_points = 1000
    points_inside, points_outside = generate_points(num_points)
    pi_estimate = calculate_pi(points_inside, num_points)
    plot_points(points_inside, points_outside, num_points, pi_estimate)
    print(f"Estimated Pi: {pi_estimate}")

if __name__ == "__main__":
    main()

この結果は以下のようになります。
全然100個程度では全然近似できないこともありますが、ある程度近い値がでるのではないでしょうか？
main関数の中に書いているnum_pointsの数を1000、10000と増やしていくとかなり近い値になると思います。

実際に一度やってみると

1000個の点の時, Estimated Pi: 3.204
10000個の点の時, Estimated Pi: 3.1644
100000個の点の時, Estimated Pi: 3.13384
1000000個の点の時, Estimated Pi: 3.141312

となり徐々に円周率の値に近づいていることが分かります。
ただ、Pythonでは1000000個でもかなり時間がかかってしまうのでRustでもやってみましょう。

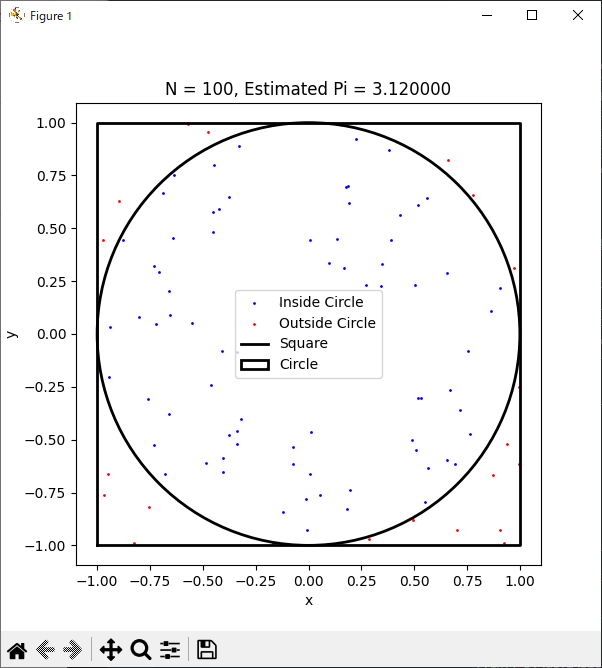
プログラムでやっていることは、

x座標、y座標ともに-1から1までの範囲でランダムに生成
その座標が円の中 (つまり、原点からの距離が1以下)なら範囲内のリストに追加、範囲外なら範囲外のリストに追加しています。(ここまでgenerate_points関数)
そのリストから円内の点の個数と、すべての点の個数から前の章で紹介した式を計算し、円周率の推定値を算出します。(calculate_pi関数)

plot_points関数で範囲内の点と、範囲外の点をグラフに描画しています。

Rustで求めてみよう

Rust版ではグラフの描画はなしで、モンテカルロ法で円周率だけを求めてみたいと思います。

use rand::Rng;

fn calculate_pi(num_samples: u32) -> f64 {
    let mut points_inside_circle = 0;

    for _ in 0..num_samples {
        // (-1,1)の範囲でランダムに点を生成
　　  // rand::random::<f64>() が0以上1未満の数値を生成するため
        // 2倍して1を引いて(-1,1)の範囲の数値が出るようにしている
        let x: f64 = rand::random::<f64>() * 2.0 - 1.0;
        let y: f64 = rand::random::<f64>() * 2.0 - 1.0;

        // 点が円の中にあるかどうかを判定
        if x * x + y * y <= 1.0 {
            points_inside_circle += 1;
        }
    }

    // 円の中に入った点の割合を計算し、πを近似
    let pi_approximation = 4.0 * (points_inside_circle as f64 / num_samples as f64);
    pi_approximation
}

fn main() {
    let num_samples = 100_000_000;
    let pi_estimate = calculate_pi(num_samples);
    println!("Estimated π: {}", pi_estimate);
}

実行した結果は

Estimated π: 3.14166588

となり、円周率にかなり近づいていることが分かります。

ランダムな点の集まりだったはずなのに、試行回数を増やすと、そこから正確な値が浮かび上がってきました。
これは、確率論の「大数の法則」という現象のおかげなのですが、ちょっと神秘的ですね！

JavaScriptで $pi$ を求めよう

100から10000までの数値を入れて $\pi$ の近似値がどんな値になるか確かめてみましょう！

モンテカルロで円周率を推定

モンテカルロ法で円周率を推定

打つ点の個数

（10〜10000）

推定値: —

打った点: — / 円内: — / 経過時間: — ms

まとめ

今回は、「モンテカルロ法」を使って、ランダムな点を使って円周率を求めてみました。

この方法は、円周率計算だけでなく、もっと複雑な図形の面積を求めたり、金融工学で将来の株価を予測したり、物流シミュレーションだったりと、実は様々な分野で使われているパワフルな手法です。

最後まで読んで頂き、ありがとうございました！