前回の記事「指数関数って何がスゴいの? ― 爆発的増加の正体に迫る」では、指数関数が持つ、私たちの直感を超える「爆発的なパワー」を体感しましたね。
2を10回かけ合わせると1024になる。
(2^{10} = 1024)
このように、ある数を特定の回数だけ掛け合わせる計算は、まさに指数の得意分野です。
では、今回はこの強力な指数の”逆”を考えてみましょう。
例えば、こう問いかけられたらどうでしょうか?
「243という数を作るには、3を一体何回かけ合わせれば良いでしょう?」
これは、
3^x = 243
を満たす「xを探す」問題です。
この「~乗」の部分、つまり指数を探し出すための、もっとスマートで強力な道具があるんです。
今回の記事では、この指数の「逆の問い」に答えるための、対数の正体に迫ります。
なぜ指数と対数が「裏表の関係」なのか、その秘密を図で解き明かしていきます。
対数の正体は「指数探し」
私たちは「3を何乗すれば243になるか?」という、指数とは”逆”の問いに直面しました。
この「~乗」の部分、つまり指数がいくつになるかを求めるために、非常に便利な記号があります。
それが、今回の主役である対数(logarithm)で、記号でlogと書きます。
言葉で覚えるより、指数と対数の関係を並べてみましょう。
■指数での表現
a^p = M
「底 a を p 乗すると M になる。」
■対数での表現
\log_aM = p
「底 a を M にするためには p 乗する必要がある。」
見比べると、構造が掴めてきませんか?
対数の正体 :
「底を何乗したら、その数(真数)になるか?」
その「何乗」の部分、つまり”指数”を探し出すための計算。
logの右下にある小さな数字が底(てい)、その隣の大きな数値が真数(しんすう)です。
そして、対数の計算結果こそが、元の指数表現における指数そのものです。
ここで、数学の言葉を使って厳密な定義も確認しておきましょう。
a>0,~a \neq 1, ~M > 0に対して、\log_a M = p \overset{\mathrm{def}}{\iff} a^p = M
いくつか例題を解いて、「指数探し」の感覚を掴みましょう。
(1) \log_2 8
これは「2を何乗したら8になりますか?」という問いです。
2 \times 2 \times 2 = 8なので、答えは3になります。
(2) \log_3 243
これは上で出てきましたね。
3 \times 3 \times 3 \times 3 \times 3 = 243なので、答えは5になります。
(3) \log_{10} 0.1
これは「10を何乗したら0.1になりますか?」という問いです。
0.1 = \frac{1}{10}で、指数では 10^{-1}でした。
よって、答えは-1になります。
さて、鋭い方はこう思ったかもしれません。
「結局、頭の中で『何回かけ算するか』を探しているだけなら、新しい記号を覚える分手間が増えているのでは?」と。
「何乗するかを調べるため」だけに対数を使うのであれば、その通りかもしれません。
しかし、対数が「強力な道具」と呼ばれる理由は別にあります。
1つは、対数logという名前を定義することで、面倒な計算をコンピューターや計算機に任せることができる点です。手計算では不可能な\log_3 1000のような計算も、プログラムなら一瞬です。
そして、もう一つが対数法則という強力なルールの存在です。
これを使うと、巨大な数の「掛け算」を簡単な「足し算」に変えたり、方程式を解く上で厄介な肩の上の指数を「掛け算の形で地上に降ろす」といった、まさに魔法のような計算が可能になります。
グラフで見る!指数関数と対数関数の「鏡写しの関係」
これまでで対数の正体が「指数探し」の計算であることを学びました。
ここからは「なぜ指数と対数は”逆”の関係なのか?」ということについて、グラフを使って迫っていきましょう。
まず、「指数のグラフを描いてみよう ―「数をかける」とどう変化する?」にて指数関数を定義しました。
ここでは代表としてy = 2^xのグラフを考えてみましょう。
xが大きくなると、爆発的にyの値が大きくなっていく、右肩上がりのカーブを描くグラフでした。
ここで、数学の世界における「逆関数」という考え方を導入します。
逆関数という新しい言葉が出てきましたが、難しく考える必要はありません。
逆関数とは、元の関数のxとyの役割を、そのまま入れ替えたものです。
元の関数 :
y = 2^x
このxとyを入れ替えると
逆関数 :
x = 2^y
が出てきます。
この式をよく見ると、「2をy乗するとxになる」という意味です。
今、変数がxなので、上の式はxを入力すると2を何乗すればよいかという値であるyが出力されることになります。
つまり、「ある数にするために必要な指数を求める」式になっていて、これが今まで学んできた対数の定義そのものになります。
つまり、上の式を書き換えると
y = log_2 x
となり、これが「対数関数」と呼ばれるものです。
さて、xとyを入れ替える操作は、グラフの世界では「y=xに関して、グラフを線対称に折り返す」という非常に美しい振る舞いをします。
その様子をPythonにて見てみましょう!
import numpy as np
import matplotlib.pyplot as plt
import math
def plot_exp_func(base):
"""底 base の指数関数 y = base^x をプロットする"""
x = np.linspace(-4, 4, 400)
# 指数関数を計算
y = base ** x
plt.plot(x, y, label=rf"$y={base}^{{x}}$", color='royalblue', linewidth=2.5)
return x, y # 拡張性のため
def plot_log_func(base):
"""底 base の対数関数 y = log_{base} x をプロットする(Numpy版)"""
x = np.linspace(0.05, 16, 400)
# 底の変換公式(第4章で後述)を使い、Numpyのlogで一括計算
y = np.log(x) / np.log(base)
plt.plot(x, y, label=rf"$y=\log_{base}{{x}}$", color='darkorange', linewidth=2.5)
return x, y
def plot_linear_func(slope, intercept):
"""1次関数 y = ax + b をプロットする関数"""
x = np.linspace(-4, 16, 100)
# 一次関数を計算
y = slope * x + intercept
plt.plot(x, y, label=rf"$y={slope}x + {intercept}$", color='green', linestyle='--')
return x, y
def setup_graph(title, xlabel="x", ylabel="y"):
"""グラフの基本的な装飾を設定する関数"""
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.axhline(y=0, color='black', linewidth=1.5) # x軸
plt.axvline(x=0, color='black', linewidth=1.5) # y軸
plt.grid(True)
plt.legend()
plt.show()
if __name__ == '__main__':
# 日本語フォントの設定
plt.rcParams['font.family'] = 'Meiryo'
# 数式部分をより美しく表示するためのフォント設定
plt.rcParams['mathtext.fontset'] = 'cm'
# グラフを正方形にして、対称性を分かりやすくする
plt.figure(figsize=(8, 8))
plt.gca().set_aspect('equal', adjustable='box')
# --- 1. 指数関数 y = 2^x の描画 (青色) ---
plot_exp_func(2)
# --- 2. 対数関数 y = log₂(x) の描画 (オレンジ色) ---
plot_log_func(2)
# --- 3. 鏡となる直線 y = x の描画 (緑色の破線) ---
plot_linear_func(1, 0)
setup_graph('指数関数と対数関数の「鏡写し」の関係')
実行すると以下のようなグラフが表示されます。
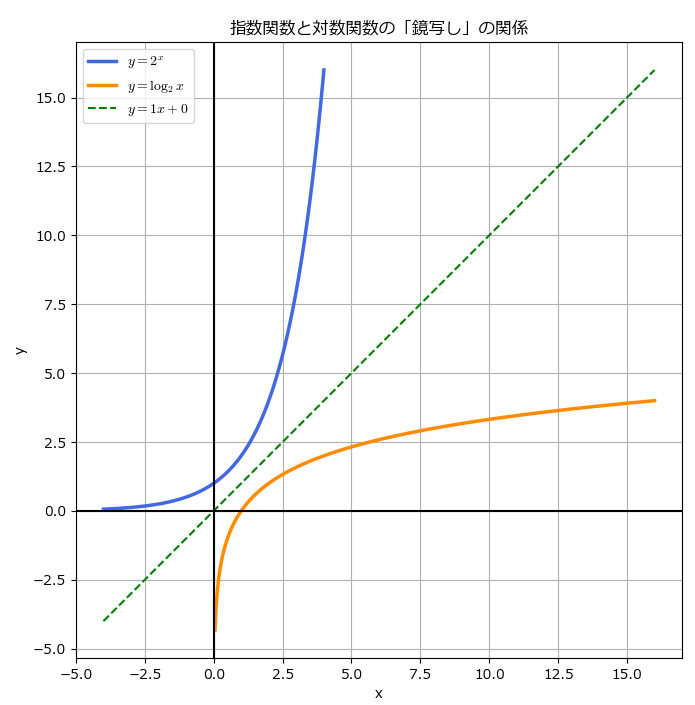
このグラフを観察すると、青い指数関数の曲線と、オレンジの対数関数の曲線が、緑の破線を鏡として反対側に映り込んでいることが分かります。
例えば、
- 指数関数上には点(3, 8)がありますが、(2^3=8なので)
- 対数関数上には点(8, 3)があります。(\log_2 8 = 3なので)
このように座標xとyを入れ替えた点が、必ずもう一方のグラフの上に乗っています。
この「鏡写しの関係」こそ、指数関数と対数関数が互いに逆関数であることの視覚的な証明になります。
対数法則の秘密 – なぜ掛け算が足し算になるのか?
対数が計算を楽にする強力な道具であることをお話しました。
その理由が「対数法則」です。
これから対数法則の1つ1つを順番に見ていきましょう!
これ以降、a,b,M,N,rを数、a \neq 1, b \neq 1, M > 0, N>0とします。
法則① : 掛け算を足し算に、割り算を引き算に
\log_a MN = \log_a M + \log_a N \\ \log_a \frac{M}{N} = \log_a M - \log_a N
この式が成り立つ理由を見てみましょう。
x = \log_a M, y = \log_a Nとします。
対数の定義より、a^x = M, a^y = Nとなります。
ここで、MNを考えるとMN = a^x a^yです。
指数法則のa^x a^y = a^{x+y}を使うと、
MN = a^{x+y}となります。
再度、対数の定義を考えると、\log_a MN = x + y = \log_a M + \log_a Nが成り立ちます。
同じように指数法則から、\frac{M}{N} = \frac{a^x}{a^y} = a^{x-y}なので、\log_a \frac{M}{N} = x – y = \log_a M – \log_a Nが成り立ちます。
法則② : 厄介な「べき乗」を、「掛け算に」
\log_a M^r = r \log_a M
x = \log_aMとおくと、対数の定義よりM = a^xが成り立ちます。
M^r = (a^x)^r = a^{xr}なので、再度対数の定義を使って、
xr = \log_a M^rとなります。
最初にx = \log_aMと置いたので、xr = r\log_aMです。
以上より、\log_a M^r = xr = r\log_aMが成り立ちます。
対数法則が便利な理由
この法則がなぜ便利なのか例をあげたいと思います。
現代では計算機があるので、そこまでは便利に感じないかもしれませんが、
例えば、「 (7.239 \times 10^{15} ) \times (4.681 \times 10^{12})を計算せよ」という例題を考えます。
ステップごとに見てきます。
Step1: logを取る
\log_{10} \{ (7.239 \times 10^{15} ) \times (4.681 \times 10^{12}) \}
Step 2: 対数法則①を使う
logの中の掛け算は足し算に変わります :
\log_{10} \{ (7.239 \times 10^{15} ) \times (4.681 \times 10^{12}) \} = \log_{10} (7.239 \times 10^{15} ) + \log_{10}(4.681 \times 10^{12})
さらに
\log_{10} (7.239 \times 10^{15} ) = \log_{10} 7.239 + \log_{10} 10^{15} = \log_{10} 7.239 + 15
\log_{10}(4.681 \times 10^{12}) = \log_{10} 4.681 + \log_{10} 10^{12} = \log_{10} 4.681 + 12
Step 3: 対数表で\log_{10}の値を取得する
ちなみに、底が10の対数を常用対数と呼び、数学や科学の分野でよく使われます。
今行っている計算を進めるために、常用対数表というものが登場します。
(このブログの一番最後に小数第2位までの常用対数表を載せています。)
この表の見方ですが、一番左の数値が小数第1位までを表し、上の数値が小数第2位を表していて、その数値の\log_{10}での値が表の中の数値となります。
例えば、\log_{10} 1.33を調べたい場合、左の1.3と上の3が交わる場所が\log_{10} 1.33の値0.1239になります。
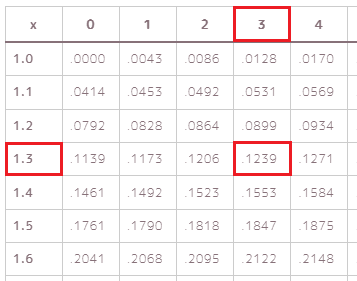
この対数表を使って、\log_{10} 7.239と\log_{10} 4.681の値を調べると、
\log_{10} 7.239 \fallingdotseq 0.8596
\log_{10} 4.681 \fallingdotseq 0.6704
となります。
Step 4: 足し算をして計算
\log_{10} 7.239 + 15 = 0.8596 + 15 = 15.8596
\log_{10} 4.681 + 12 = 0.6704 + 12 = 12.6704
となり、
\log_{10} \{ (7.239 \times 10^{15} ) \times (4.681 \times 10^{12}) \} = 28.53
Step 5: 対数の定義から指数の形に戻す
対数の定義より、(7.239 \times 10^{15} ) \times (4.681 \times 10^{12}) = 10^{28.53} = 10^{0.53} \times 10^{28} です。
Step 6: 整数部分は桁に、小数部分を常用対数表で取得
今知りたいのは10^{0.53}の値です。
なので、 a = 10^{0.53}と置いて、logを取ると、
\log_{10} a = \log_{10} 10^{0.53} = 0.53となります。
常用対数表から0.53付近の値を調べると、おおよそ3.388になります :
10^{0.53} \fallingdotseq 3.388
Step 7: 答え
以上より、(7.239 \times 10^{15} ) \times (4.681 \times 10^{12}) = 3.388 \times \times 10^{28} となります。
常用対数表を用いることで複雑な計算をほとんどすることなく、大きな数通しの掛け算のおおよその値を計算することができます。
これが対数法則が強力である理由です。
法則③ : 底を好きに変えることができる「底の変換公式」
底の変換公式も対数法則に入れてよいものですが、ここで紹介します。
前に出てきたPythonのソースコードでもこの公式を使用しています。
\log_a M = \frac{\log_b M}{\log_b a}
x = \log_aMとおくと、対数の定義よりM = a^xが成り立ちます。
ここで、この両辺に底がbの対数をとります :
\log_b M = \log_b a^x
法則②を考えると右辺は x \log_b aとなります。
この両辺を\log_b aで割ります。
\frac{\log_b M}{\log_b a} = x = \log_a Mこれで底の変換公式が成り立つことが分かります。
対数のパワー : 巨大な世界を「人間の物差し」に
自然界や経済の現象は、「1,2,3,…]と等間隔に増える線形なものだけでなく、「10,100,1000,…」のように増えていく指数なものであふれています。
それを理解するための物差しが「対数」になります。
対数での物差しと普通の物差しを比べてみましょう。
- 普通の物差し : 「1と2の間の距離」と「9と10の間の距離」は同じ
- 対数の物差し : 「1と10の間の距離」と「100と1000の間の距離」は同じ
対数の物差しでは、対数法則より掛け算を足し算に変えることができるため、非常に大きい数値から小さい数値までを1枚のグラフや1つの指標で表現することができるようになります。
地震のマグニチュード
ニュースで耳にする「マグニチュード」。
これは、地震のエネルギーを対数で表した指標です。
マグニチュードとエネルギーの関係を表す経験式は以下になります。
ここでは、Eは放射地震エネルギー(単位:ジュール)、M_{\omega}はマグニチュードを表しています。
\log_{10} E = 4.8 + 1.5M_{\omega}- マグニチュードが1増えると、エネルギーは約32倍になります。
- マグニチュードが2増えると、エネルギーはなんと32 x 32 ≒ 1000倍も違います。
マグニチュードでみると5と7では、数値上はたった「2」の違いですが、実際のエネルギーは1000倍も違うのです。
対数の物差しがなければ、この大きなエネルギー差を簡単な数値で比較することができなくなります。
実際に、上の式からマグニチュード5と7のエネルギーの差を計算してみます。
マグニチュード5の時のエネルギーをE_5、マグニチュード7の時のエネルギーをE_7とします。
- \log_{10} E_5 = 4.8 + 1.5 \times 5 = 12.3
- \log_{10} E_7 = 4.8 + 1.5 \times 7 = 15.3
対数の定義からE_5とE_7の値を出して計算しても良いのですが、今回は対数法則を上手く使います。
\log_{10}(\frac{E_7}{E_5}) =\log_{10}E_7 - \log_{10}E_5 = 15.3 - 12.3 = 3ここで対数の定義より、
\frac{E_7}{E_5} = 10^3 = 1000
が分かります。
ちなみに、
E_5 \fallingdotseq 10^{12} \times 1.995262315
E_7 \fallingdotseq 10^{15} \times 1.995262315
です。
対数という物差しがあるおかけで、エネルギーが1000倍違うという巨大な差を、マグニチュードが2違うというシンプルな差として認識ができます。
音の大きさのデシベル (dB)
静かな図書館 (約40dB)とロックコンサート(約120dB)の差は80dBです。
しかし、実際の音のエネルギー(音圧)の差は、なんと100,000,000倍(1億倍)にもなります。
音の大きさ「デシベル(dB)」は、物理的な「音圧(Pa)」から次のように計算されます。
\textrm{dB} = 20 \times \log_{10}(\frac{\textrm{測定した音圧}}{\textrm{基準となる音圧}})
この式では、「音圧の比」に対して対数をとることで、デシベルという単位に変換していることがポイントです。
静かな図書館とロックコンサートの物理的なエネルギーの差を実際に計算してみます。
P_0を基準となる音圧、P_{concert}がロックコンサートの音圧、P_{library}が静かな図書館の音圧とします。
デシベルの定義式から
80 = 20 \times \{ \log_{10}(\frac{P_{concert}}{P_0}) - \log_{10}(\frac{P_{library}}{P_0}) \} \\= 20\log_{10}(\frac{P_{concert}}{P_{library}})途中に対数法則を使っています。
これより、
4 = \log_{10}(\frac{P_{concert}}{P_{library}})となり、対数の定義より
\frac{P_{concert}}{P_{library}} = 10^4 = 10,000となり、音圧(空気の振動の振幅)だけで、すでに1万倍も違うことが分かります。
さらに、音のエネルギーは音圧の2乗に比例するので、エネルギーの比は
\textrm{エネルギーの比} = (\frac{P_{concert}}{P_{library}})^2 = 10^8 = 100,000,000となり、1億倍であることが分かります。
まとめ
今回の記事では、指数の「逆の問い」から出発し、その最高の相棒である対数の正体に迫りました。
この記事を通して、私たちは対数が持つ3つの重要な顔を発見しました。
- 「指数探し」
対数の定義は、a^p=Mにおける「指数p」を見つけ出すための、シンプルで強力な道具でした。 - 計算を楽にするツール
複雑な掛け算を足し算に変える対数法則は、歴史的に天文学などの計算を劇的に加速させました。
これは、対数が指数の世界と深く繋がっているからこそ使える強力なツールです。 - 指数関数の「鏡写し」の姿
グラフを描くことで、対数関数は指数関数の姿を直線y=xという鏡に映した、美しい線対称の(逆関数の)関係にあることを視覚的に理解しました。
指数と対数。
これらは決して別々の存在ではなく、常にお互いを写し合う「裏表一体」の関係です。
この関係性を理解することで、私たちは初めて指数や対数という道具を真に使いこなすことができるのです。
最後までご覧いただき、ありがとうございました。
数学の世界をより深く、面白いものにするきっかけとなれれば幸いです!
(参考)常用対数表(小数第2位まで)
\log_{10}xの値
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.0 | .0000 | .0043 | .0086 | .0128 | .0170 | .0212 | .0253 | .0294 | .0334 | .0374 |
| 1.1 | .0414 | .0453 | .0492 | .0531 | .0569 | .0607 | .0645 | .0682 | .0719 | .0755 |
| 1.2 | .0792 | .0828 | .0864 | .0899 | .0934 | .0969 | .1004 | .1038 | .1072 | .1106 |
| 1.3 | .1139 | .1173 | .1206 | .1239 | .1271 | .1303 | .1335 | .1367 | .1399 | .1430 |
| 1.4 | .1461 | .1492 | .1523 | .1553 | .1584 | .1614 | .1644 | .1673 | .1703 | .1732 |
| 1.5 | .1761 | .1790 | .1818 | .1847 | .1875 | .1903 | .1931 | .1959 | .1987 | .2014 |
| 1.6 | .2041 | .2068 | .2095 | .2122 | .2148 | .2175 | .2201 | .2227 | .2253 | .2279 |
| 1.7 | .2304 | .2330 | .2355 | .2380 | .2405 | .2430 | .2455 | .2480 | .2504 | .2529 |
| 1.8 | .2553 | .2577 | .2601 | .2625 | .2648 | .2672 | .2695 | .2718 | .2742 | .2765 |
| 1.9 | .2788 | .2810 | .2833 | .2856 | .2878 | .2900 | .2923 | .2945 | .2967 | .2989 |
| 2.0 | .3010 | .3032 | .3054 | .3075 | .3096 | .3118 | .3139 | .3160 | .3181 | .3201 |
| 2.1 | .3222 | .3243 | .3263 | .3284 | .3304 | .3324 | .3345 | .3365 | .3385 | .3404 |
| 2.2 | .3424 | .3444 | .3464 | .3483 | .3502 | .3522 | .3541 | .3560 | .3579 | .3598 |
| 2.3 | .3617 | .3636 | .3655 | .3674 | .3692 | .3711 | .3729 | .3747 | .3766 | .3784 |
| 2.4 | .3802 | .3820 | .3838 | .3856 | .3874 | .3892 | .3909 | .3927 | .3945 | .3962 |
| 2.5 | .3979 | .3997 | .4014 | .4031 | .4048 | .4065 | .4082 | .4099 | .4116 | .4133 |
| 2.6 | .4150 | .4166 | .4183 | .4200 | .4216 | .4232 | .4249 | .4265 | .4281 | .4298 |
| 2.7 | .4314 | .4330 | .4346 | .4362 | .4378 | .4393 | .4409 | .4425 | .4440 | .4456 |
| 2.8 | .4472 | .4487 | .4502 | .4518 | .4533 | .4548 | .4564 | .4579 | .4594 | .4609 |
| 2.9 | .4624 | .4639 | .4654 | .4669 | .4683 | .4698 | .4713 | .4728 | .4742 | .4757 |
| 3.0 | .4771 | .4786 | .4800 | .4814 | .4829 | .4843 | .4857 | .4871 | .4886 | .4900 |
| 3.1 | .4914 | .4928 | .4942 | .4955 | .4969 | .4983 | .4997 | .5011 | .5024 | .5038 |
| 3.2 | .5051 | .5065 | .5079 | .5092 | .5105 | .5119 | .5132 | .5145 | .5159 | .5172 |
| 3.3 | .5185 | .5198 | .5211 | .5224 | .5237 | .5250 | .5263 | .5276 | .5289 | .5302 |
| 3.4 | .5315 | .5328 | .5340 | .5353 | .5366 | .5378 | .5391 | .5403 | .5416 | .5428 |
| 3.5 | .5441 | .5453 | .5465 | .5478 | .5490 | .5502 | .5514 | .5527 | .5539 | .5551 |
| 3.6 | .5563 | .5575 | .5587 | .5599 | .5611 | .5623 | .5635 | .5647 | .5658 | .5670 |
| 3.7 | .5682 | .5694 | .5705 | .5717 | .5729 | .5740 | .5752 | .5763 | .5775 | .5786 |
| 3.8 | .5798 | .5809 | .5821 | .5832 | .5843 | .5855 | .5866 | .5877 | .5888 | .5899 |
| 3.9 | .5911 | .5922 | .5933 | .5944 | .5955 | .5966 | .5977 | .5988 | .5999 | .6010 |
| 4.0 | .6021 | .6031 | .6042 | .6053 | .6064 | .6075 | .6085 | .6096 | .6107 | .6117 |
| 4.1 | .6128 | .6138 | .6149 | .6160 | .6170 | .6180 | .6191 | .6201 | .6212 | .6222 |
| 4.2 | .6232 | .6243 | .6253 | .6263 | .6274 | .6284 | .6294 | .6304 | .6314 | .6325 |
| 4.3 | .6335 | .6345 | .6355 | .6365 | .6375 | .6385 | .6395 | .6405 | .6415 | .6425 |
| 4.4 | .6435 | .6444 | .6454 | .6464 | .6474 | .6484 | .6493 | .6503 | .6513 | .6522 |
| 4.5 | .6532 | .6542 | .6551 | .6561 | .6571 | .6580 | .6590 | .6599 | .6609 | .6618 |
| 4.6 | .6628 | .6637 | .6646 | .6656 | .6665 | .6675 | .6684 | .6693 | .6702 | .6712 |
| 4.7 | .6721 | .6730 | .6739 | .6749 | .6758 | .6767 | .6776 | .6785 | .6794 | .6803 |
| 4.8 | .6812 | .6821 | .6830 | .6839 | .6848 | .6857 | .6866 | .6875 | .6884 | .6893 |
| 4.9 | .6902 | .6911 | .6920 | .6928 | .6937 | .6946 | .6955 | .6964 | .6972 | .6981 |
| 5.0 | .6990 | .6998 | .7007 | .7016 | .7024 | .7033 | .7042 | .7050 | .7059 | .7067 |
| 5.1 | .7076 | .7084 | .7093 | .7101 | .7110 | .7118 | .7126 | .7135 | .7143 | .7152 |
| 5.2 | .7160 | .7168 | .7177 | .7185 | .7193 | .7202 | .7210 | .7218 | .7226 | .7235 |
| 5.3 | .7243 | .7251 | .7259 | .7267 | .7275 | .7284 | .7292 | .7300 | .7308 | .7316 |
| 5.4 | .7324 | .7332 | .7340 | .7348 | .7356 | .7364 | .7372 | .7380 | .7388 | .7396 |
| 5.5 | .7404 | .7412 | .7419 | .7427 | .7435 | .7443 | .7451 | .7459 | .7466 | .7474 |
| 5.6 | .7482 | .7490 | .7497 | .7505 | .7513 | .7520 | .7528 | .7536 | .7543 | .7551 |
| 5.7 | .7559 | .7566 | .7574 | .7582 | .7589 | .7597 | .7604 | .7612 | .7619 | .7627 |
| 5.8 | .7634 | .7642 | .7649 | .7657 | .7664 | .7672 | .7679 | .7686 | .7694 | .7701 |
| 5.9 | .7709 | .7716 | .7723 | .7731 | .7738 | .7745 | .7752 | .7760 | .7767 | .7774 |
| 6.0 | .7782 | .7789 | .7796 | .7803 | .7810 | .7818 | .7825 | .7832 | .7839 | .7846 |
| 6.1 | .7853 | .7860 | .7868 | .7875 | .7882 | .7889 | .7896 | .7903 | .7910 | .7917 |
| 6.2 | .7924 | .7931 | .7938 | .7945 | .7952 | .7959 | .7966 | .7973 | .7980 | .7987 |
| 6.3 | .7993 | .8000 | .8007 | .8014 | .8021 | .8028 | .8035 | .8041 | .8048 | .8055 |
| 6.4 | .8062 | .8069 | .8075 | .8082 | .8089 | .8096 | .8102 | .8109 | .8116 | .8122 |
| 6.5 | .8129 | .8136 | .8142 | .8149 | .8156 | .8162 | .8169 | .8176 | .8182 | .8189 |
| 6.6 | .8195 | .8202 | .8209 | .8215 | .8222 | .8228 | .8235 | .8241 | .8248 | .8254 |
| 6.7 | .8261 | .8267 | .8274 | .8280 | .8287 | .8293 | .8299 | .8306 | .8312 | .8319 |
| 6.8 | .8325 | .8331 | .8338 | .8344 | .8351 | .8357 | .8363 | .8370 | .8376 | .8382 |
| 6.9 | .8388 | .8395 | .8401 | .8407 | .8414 | .8420 | .8426 | .8432 | .8439 | .8445 |
| 7.0 | .8451 | .8457 | .8463 | .8470 | .8476 | .8482 | .8488 | .8494 | .8500 | .8506 |
| 7.1 | .8513 | .8519 | .8525 | .8531 | .8537 | .8543 | .8549 | .8555 | .8561 | .8567 |
| 7.2 | .8573 | .8579 | .8585 | .8591 | .8597 | .8603 | .8609 | .8615 | .8621 | .8627 |
| 7.3 | .8633 | .8639 | .8645 | .8651 | .8657 | .8663 | .8669 | .8675 | .8681 | .8686 |
| 7.4 | .8692 | .8698 | .8704 | .8710 | .8716 | .8722 | .8727 | .8733 | .8739 | .8745 |
| 7.5 | .8751 | .8756 | .8762 | .8768 | .8774 | .8779 | .8785 | .8791 | .8797 | .8802 |
| 7.6 | .8808 | .8814 | .8820 | .8825 | .8831 | .8837 | .8842 | .8848 | .8854 | .8859 |
| 7.7 | .8865 | .8871 | .8876 | .8882 | .8887 | .8893 | .8899 | .8904 | .8910 | .8915 |
| 7.8 | .8921 | .8927 | .8932 | .8938 | .8943 | .8949 | .8954 | .8960 | .8965 | .8971 |
| 7.9 | .8976 | .8982 | .8987 | .8993 | .8998 | .9004 | .9009 | .9015 | .9020 | .9025 |
| 8.0 | .9031 | .9036 | .9042 | .9047 | .9053 | .9058 | .9063 | .9069 | .9074 | .9079 |
| 8.1 | .9085 | .9090 | .9096 | .9101 | .9106 | .9112 | .9117 | .9122 | .9127 | .9133 |
| 8.2 | .9138 | .9143 | .9149 | .9154 | .9159 | .9165 | .9170 | .9175 | .9180 | .9186 |
| 8.3 | .9191 | .9196 | .9201 | .9206 | .9212 | .9217 | .9222 | .9227 | .9232 | .9238 |
| 8.4 | .9243 | .9248 | .9253 | .9258 | .9263 | .9269 | .9274 | .9279 | .9284 | .9289 |
| 8.5 | .9294 | .9299 | .9304 | .9309 | .9315 | .9320 | .9325 | .9330 | .9335 | .9340 |
| 8.6 | .9345 | .9350 | .9355 | .9360 | .9365 | .9370 | .9375 | .9380 | .9385 | .9390 |
| 8.7 | .9395 | .9400 | .9405 | .9410 | .9415 | .9420 | .9425 | .9430 | .9435 | .9440 |
| 8.8 | .9445 | .9450 | .9455 | .9460 | .9465 | .9469 | .9474 | .9479 | .9484 | .9489 |
| 8.9 | .9494 | .9499 | .9504 | .9509 | .9513 | .9518 | .9523 | .9528 | .9533 | .9538 |
| 9.0 | .9542 | .9547 | .9552 | .9557 | .9562 | .9566 | .9571 | .9576 | .9581 | .9586 |
| 9.1 | .9590 | .9595 | .9600 | .9605 | .9609 | .9614 | .9619 | .9624 | .9628 | .9633 |
| 9.2 | .9638 | .9643 | .9647 | .9652 | .9657 | .9661 | .9666 | .9671 | .9675 | .9680 |
| 9.3 | .9685 | .9689 | .9694 | .9699 | .9703 | .9708 | .9713 | .9717 | .9722 | .9727 |
| 9.4 | .9731 | .9736 | .9741 | .9745 | .9750 | .9754 | .9759 | .9763 | .9768 | .9773 |
| 9.5 | .9777 | .9782 | .9786 | .9791 | .9795 | .9800 | .9805 | .9809 | .9814 | .9818 |
| 9.6 | .9823 | .9827 | .9832 | .9836 | .9841 | .9845 | .9850 | .9854 | .9859 | .9863 |
| 9.7 | .9868 | .9872 | .9877 | .9881 | .9886 | .9890 | .9894 | .9899 | .9903 | .9908 |
| 9.8 | .9912 | .9917 | .9921 | .9926 | .9930 | .9934 | .9939 | .9943 | .9948 | .9952 |
| 9.9 | .9956 | .9961 | .9965 | .9969 | .9974 | .9978 | .9983 | .9987 | .9991 | .9996 |